はじめに

初心者が Kaggle の Titanic をやってみた第 4 回目モデル評価編やります！

（↓ これまでの記事）

• 【機械学習】初心者が Kaggle の titanic で勉強してみた
• 【機械学習】初心者が Kaggle の titanic で勉強してみた(前処理編)
• 【機械学習】初心者が Kaggle の titanic で勉強してみた(アルゴリズム選定編)

このシリーズはこれでラストです！！

よーーーーやく終わります。

前回は、いくつかのアルゴリズムを検証データで評価し、ロジスティック回帰とランダムフォレストにアルゴリズムを絞りました。

さらに、この二つのアルゴリズムに対してハイパーパラメータチューニングを行い、性能の向上を試みました。 しかし、結果はそんなによくなかった。。。

そこで、今回は特徴量エンジニアリングを行なって、モデルの精度を向上させたいと思います！

やっていくなかで、これまでのコードがいろいろよくないアプローチをしていたことに気づいたので、それらはいったん忘れてください。。

これを読み終わったあとに前のやつを見返すと無駄なことをやってるいことに気づくと思います。

特徴量エンジニアリング

特徴量エンジニアリングは、モデルの精度向上のために、データから特徴量を選択・加工・生成する作業だと自分は考えています。

参考書籍の「Python ではじめる機械学習」では特徴量エンジニアリングは

「特定のアプリケーションに対して、最良のデータ表現を模索すること」

出典：Andreas C. Muller、Sarah Guido 著、中田 秀基 訳「Python ではじめる機械学習」

とあります。

私も今回いろいろ試してみてこの最良のデータ表現の模索というのがぴったりだなと思っています。

それでは、どのようにこのよいデータ表現を見つければいいのか。

私が現在考えてるアプローチは以下のものです。

• 数値データをビニングしてカテゴライズ
• 数値データの正規化 or 標準化
• 新しい特徴量の作成（問題に基づいて作成）

今回の titanic のような分類問題の場合、まず1のアプローチをやってみる。そのために、数値データであるFareのヒストグラムをもう一度確認してみる。

import pandas as pd
import matplotlib.pyplot as plt
TRAIN_DATA_FILE = "train.csv"
train_data = pd.read_csv(TRAIN_DATA_FILE)
y = train_data["Survived"]
train_data["Fare"].hist(bins=50, figsize=(10,5))
plt.title("Fare histgram")
plt.xlabel("Fare")
plt.show()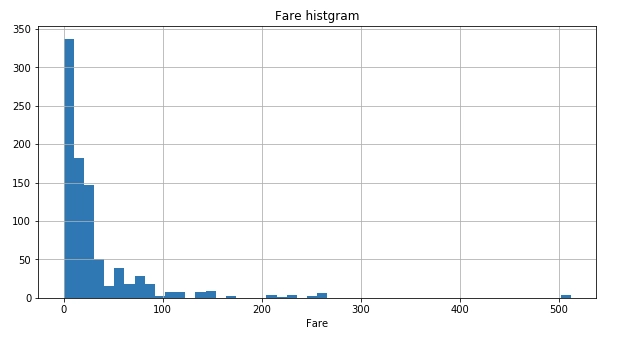

0〜500 までの広い値をとることがわかる。 さらに以下のSurvived={0, 1}がFareの値とどのように対応しているのかカウントして平均をとった情報をみてみる。

print (train_data[["Fare", "Survived"]].groupby(['Fare'], as_index=False).mean().head(10))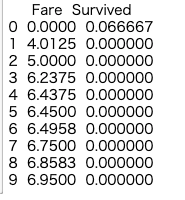

ほとんどのFareの値で十分なデータがないことがわかる。

というより、こんなに細かく値を区切って生存したかどうかを判断するかはおかしい。

おそらく、料金と生存者の相関はあるだろう。しかし、ここまで細かい値の違いで傾向は抽出できないはず。

そこで、ある程度値をまとめあげてカテゴライズすることを考える。 （参考：https://www.kaggle.com/sinakhorami/titanic-best-working-classifier） リンクが切れてました（2019/08/22 　追記）

def FE_fare(data):
    # qcutで各ビンに含まれる個数が等しくなるようにビン分割する
    data['CategoricalFare'] = pd.qcut(data['Fare'], 4)
    data.loc[data['Fare'] <= 7.91, 'Fare']                         = 0
    data.loc[(data['Fare'] > 7.91) & (data['Fare'] <= 14.454), 'Fare'] = 1
    data.loc[(data['Fare'] > 14.454) & (data['Fare'] <= 31), 'Fare']   = 2
    data.loc[ data['Fare'] > 31, 'Fare']        =3
FE_fare(train_data)
print (train_data[['CategoricalFare', 'Survived']].groupby(['CategoricalFare'], as_index=False).mean().head())

明らかに料金が高い方が生存の割合が高いのがわかる。

同様にAgeのデータも処理していく。 まず、ヒストグラムは以下の通り。

train_data["Age"].hist(bins=50, figsize=(10,5))
plt.title("Age histgram")
plt.xlabel("Age")
plt.show()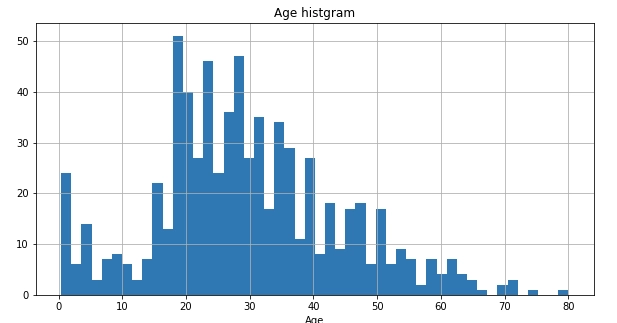

0〜80 歳と広い値をとりうることがわかる。また、前処理編でみたように、Ageデータは欠損値があるのでそれを補填する必要がある。

ただし、以前の中央値で欠損をうめるのはよくない。 補填後の以下の分布をみればわかる。

train_data["Age"] = train_data["Age"].fillna(train_data["Age"].median())
train_data["Age"].hist(bins=50, figsize=(10,5))
plt.title("Age histgram")
plt.xlabel("Age")
plt.show()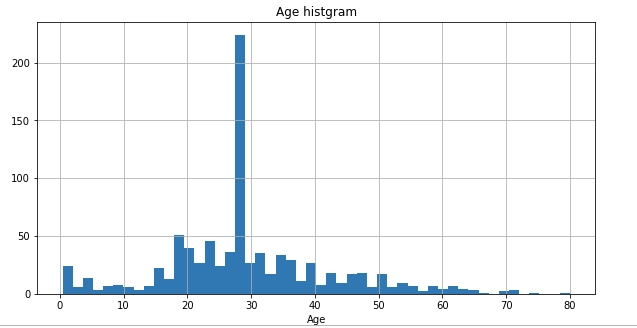

見てのとおり補填した中央値だけ突き抜けてしまう。

なので、データの分布から値を生成して欠損値をうめる。このアプローチも上と同様に以下のコードを参考にさせていただきました。

（参考：https://www.kaggle.com/sinakhorami/titanic-best-working-classifier） リンク切れでした（2019/08/22 追記）

def FE_age(data):
    age_avg        = data['Age'].mean()
    age_std        = data['Age'].std()
    age_null_count = data['Age'].isnull().sum()
    ## 平均値と平均標準偏差の間の値からからランダムに欠損分だけ選択
    age_null_random_list = np.random.randint(age_avg - age_std, age_avg + age_std, size=age_null_count)
    data['Age'][np.isnan(data['Age'])] = age_null_random_list
    data['Age'] = data['Age'].astype(int)
    data['CategoricalAge'] = pd.cut(data['Age'], 5)
    # Mapping Age
    data.loc[data['Age'] <= 16, 'Age']                         = 0
    data.loc[(data['Age'] > 16) & (data['Age'] <= 32), 'Age'] = 1
    data.loc[(data['Age'] > 32) & (data['Age'] <= 48), 'Age'] = 2
    data.loc[(data['Age'] > 48) & (data['Age'] <= 64), 'Age'] = 3
    data.loc[ data['Age'] > 64, 'Age']  = 4
FE_age(train_data)
train_data["Age"].hist(bins=50, figsize=(10,5))
plt.title("Age histgram")
plt.xlabel("Age")
plt.show()
print (train_data[['CategoricalAge', 'Survived']].groupby(['CategoricalAge'], as_index=False).mean().head())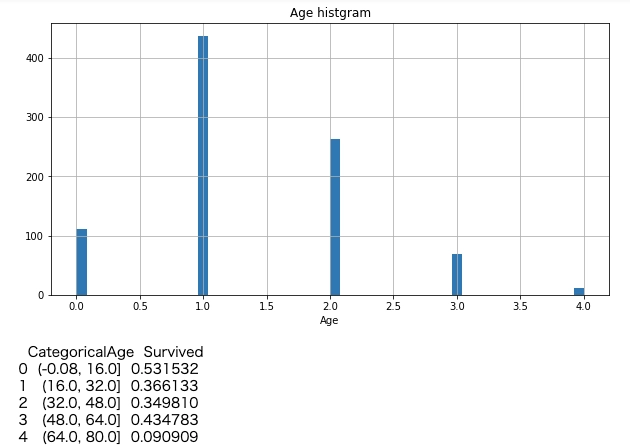

おー明らかに子供の生存率が高くて老人の生存率が低いことがわかる。 特徴とよべるものがよくでてる。

数値データに関する特徴量エンジニアリングはこれで終わり。 最初よりデータがよい表現になった気がしてる。

続いて、3のアプローチをやっていく。 今回は2のアプローチはやりません（おそらく必要ない）

新しく特徴量を作るということで、SibSpとParchから家族人数という変数を作る。 この特徴量を作る理由は、いろいろなサイトで作成しているのを見たから。

というのもあるが、生存者予測という課題なら同乗している家族人数が影響しそうなファクターであることは想像できると思う。 （こんな感じで特徴量にあたりをつけて作れるのが一流のデータサイエンティストなのかな）

def FE_family_size(data):
    # 家族サイズ
    family_size = []
    for a_tmp, b_tmp in zip(data["SibSp"], data['Parch']):
        num_family = a_tmp + b_tmp + 1
        if num_family > 4:
            num_family = 5
            family_size.append(num_family)
        else:
            family_size.append(num_family)
    data["family_size"]  = family_size
FE_family_size(train_data)
print (train_data[["family_size", "Survived"]].groupby(["family_size"], as_index=False).mean().head(10))

これもいい特徴になっている気する。

家族人数が多い方が生存者割合が低いことがわかる（5 人以上のサンプルが少ない可能性がありそう）

生成は以上。あとはEmbarkedとSexのカテゴリを整数値にする（今回はカテゴリ変数にしない）。

def FE_Embarked(data):
    data = data.fillna({'Embarked': 'S'}, inplace = True)
    data['Embarked'] = data['Embarked'].map( {'S': 1, 'C': 2, 'Q': 3} ).astype(int)
FE_Embarked(train_data)
print (train_data[["Embarked", "Survived"]].groupby(["Embarked"], as_index=False).mean().head(10))
def FE_sex_onehot(data):
    ## 性別を1カラムに
    data.loc[data["Sex"] == "female", 'Sex'] = 0
    data.loc[data["Sex"] == "male", 'Sex'] = 1
FE_sex_onehot(train_data)

ここまでやると次のような特徴量が出来上がっているはず

train_data.info()

次はいらない列をおとす。

train_data = train_data.drop(['CategoricalAge', 'CategoricalFare'], axis = 1)
drop_train_list = ['PassengerId', "Name", 'Ticket', 'Cabin', 'Survived']
def drop_columns(drop_list, data):
    data = data.drop(drop_list, axis=1)
    return data
train_data = drop_columns(drop_train_list, train_data)

これで特徴量エンジニアリングをふまえた前処理終了。

ランダムフォレストを用いた特徴量の重要度可視化

ランダムフォレストなどの決定木を用いたアルゴリズムはどの特徴量が最終的な決定に影響しているのか可視化することができる。 これで、重要そうな特徴量がわかる（あとで説明もしやすい）。

from sklearn import model_selection, metrics
X_train, X_test, y_train, y_test = model_selection.train_test_split(train_data, y, random_state=1)
# ランダムフォレスト重要度
def measure_importance_rdf(X_train, y_train, X_test, y_test):
    rf = RandomForestClassifier()
    rf.fit(X_train, y_train)
    features = pd.DataFrame()
    features['feature'] = X_train.columns
    features['importance'] = rf.feature_importances_
    features.sort_values(by=['importance'], ascending=True, inplace=True)
    features.set_index('feature', inplace=True)
    features.plot(kind='barh', figsize=(10, 5))
measure_importance_rdf(X_train, y_train, X_test, y_test)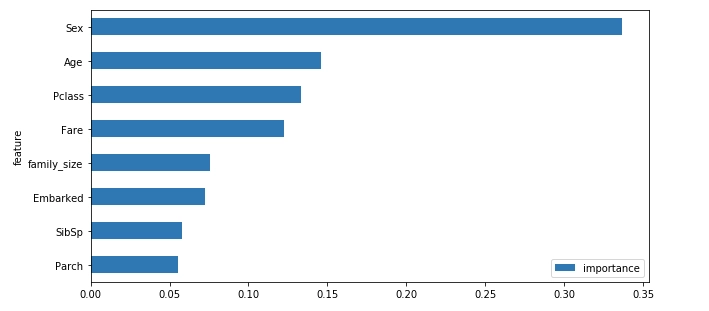

グラフを見ると、性別と年齢が大事という結果に。

これは説明がつきそうな結果ですね。緊急時は、女性と子供と金持ちが優先されるということかな。

続いて、前回同様に各種アルゴリズムに投入してみる。

from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier # K近傍法
from sklearn.svm import SVC # サポートベクターマシン
from sklearn.tree import DecisionTreeClassifier # 決定木
from sklearn.ensemble import RandomForestClassifier # ランダムフォレスト
from sklearn.ensemble import AdaBoostClassifier # AdaBoost
from sklearn.naive_bayes import GaussianNB # ナイーブ・ベイズ
def test_algorithm(X_train, X_test, y_train, y_test, classifiers, names, version):
    result = []
    for clf, name in zip(classifiers, names):
        clf.fit(X_train.values, y_train.values)
        score1 = clf.score(X_train, y_train)
        score2 = clf.score(X_test, y_test)
        fname = name + "_" + version + "{}".format(".pickle")
        result.append([score1, score2])
        with open(fname, 'wb') as f:
            pickle.dump(clf, f)
    df_result = pd.DataFrame(result, columns=['train', 'test'], index = names)
    print(df_result)
classifiers = [
    LogisticRegression(),
    KNeighborsClassifier(),
    DecisionTreeClassifier(),
    RandomForestClassifier(),
    AdaBoostClassifier(),
    GaussianNB(),
]
names = ["Logistic Regression", "Nearest Neighbors", "Decision Tree","Random Forest", "AdaBoost", "Naive Bayes"]
test_algorithm(X_train, X_test, y_train, y_test, classifiers, names, version="4")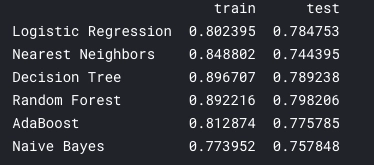

ランダムフォレスト、決定木、ロジスティック回帰がいい性能をだしてることがわかる。

前回の記事の結果と比べると、全体的に少しだけ良性能が向上しているように見える。何回か試してみた感じでも、今回のほうが安定していた。

決定木は汎化性能をあげるのが難しそうなので、ランダムフォレストとロジスティック回帰のハイパーパラメータチューニングをすることにする。

version = "3"
fname_lgr = "LogisticRegression_with_best_param_{}".format(version) + "_{}".format(".pickle")
def grid_search_lgr(X_train, y_train, X_test, y_test, fname):
    # ロジスティック回帰のパラメータ
    parameter={"C":[10**i for i in range(-2,4)],"random_state":[1, 2, 3],}
    grid_search = GridSearchCV(LogisticRegression(), parameter, cv=5)
    grid_search.fit(X_train, y_train)
    print("Best parameters : {}".format(grid_search.best_params_))
    print("Best cross-validation score : {:.3f}".format(grid_search.best_score_))
    lgr = LogisticRegression(**grid_search.best_params_)
    lgr.fit(X_train, y_train)
    with open(fname, 'wb') as f:
            pickle.dump(lgr, f)
    test_score = lgr.score(X_test, y_test)
    print("Score with best parameteras : {}".format(test_score))
grid_search_lgr(X_train, y_train, X_test, y_test, fname_lgr)

以前と同様で、チューニングしてもあまり変わらない（変わる時もあった）。 ランダムフォレストもやってみる。

version = "3"
fname_rf = "RandomForesr_with_best_param_{}".format(version) + "_{}".format(".pickle")
def grid_search_rdf(X_train, y_train, X_test, y_test, fname_rf):
    # n_estimators → 決定木の数
    # max_features → 決定木の特徴量の数
    # random_state → 乱数シード
    # max_depth → 決定木の深さ
    # min_samples_split → 決定木を分割する際のサンプル数の最小数
    parameter={
        "n_estimators":[i  for i in range(10, 100, 10)],
        "criterion":["gini","entropy"],
        "max_depth":[i for i in range(1,10,1)],
        "min_samples_split": [2, 4, 10,12,16],
        "random_state":[3]
    }
    grid_search = GridSearchCV(RandomForestClassifier(), parameter, cv=5)
    grid_search.fit(X_train, y_train)
    print("Best parameters : {}".format(grid_search.best_params_))
    print("Best cross-validation score : {:.3f}".format(grid_search.best_score_))
    rf = RandomForestClassifier(**grid_search.best_params_)
    rf.fit(X_train, y_train)
    #fname = "RandomForesr_with_best_param" + "{}".format(".pickle")
    with open(fname_rf, 'wb') as f:
            pickle.dump(rf, f)
    test_score = rf.score(X_test, y_test)
    print("Score with best parameteras : {}".format(test_score))
grid_search_rdf(X_train, y_train, X_test, y_test, fname_rf)

こっちはだいぶよくなる。

検証セットでの結果はいまいちだが。

モデルの評価

モデルの評価では、以下のことをみてみる。

• 混合行列
• 適合率、再現率、F1 スコア
• ROC 曲線

今回は次のようにこれらをまとめた関数でいっぺんに表示する。 まずはロジスティック回帰。

from sklearn.metrics import confusion_matrix, precision_score, recall_score, f1_score, roc_curve, auc
def evaluation(model, X_test, y_test):
    y_pred = model.predict(X_test)
    m = confusion_matrix(y_test, y_pred)
    print("Confusion matrix:\n{}".format(m))
    print()
    print("適合率：{:.3f}".format(precision_score(y_test, y_pred)))
    print("再現率：{:.3f}".format(recall_score(y_test, y_pred)))
    print("f1：{:.3f}".format(f1_score(y_test, y_pred)))
    y_pred = model.predict_proba(X_test)[:,1]
    fpr, tpr, thresholds = roc_curve(y_test, y_pred)
    auc_num = auc(fpr, tpr)
    plt.plot(fpr, tpr, color="blue", label="ROC curve (area = %.3f)" % auc_num)
    plt.plot([0,1], [0,1], color="black", linestyle="--")
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel("False positive rate")
    plt.xlabel("True positive rate")
    plt.legend(loc="right lower")
with open(fname_lgr, mode='rb') as fp:
    lgr = pickle.load(fp)
evaluation(lgr, X_test, y_test)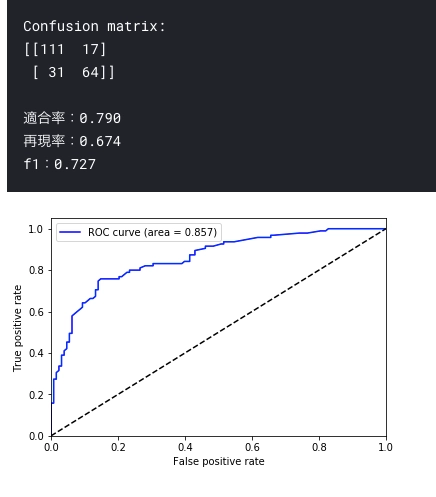

再現率低い。。

次はランダムフォレスト。

with open(fname_rf, mode='rb') as fp:
    rf = pickle.load(fp)
evaluation(rf, X_test, y_test)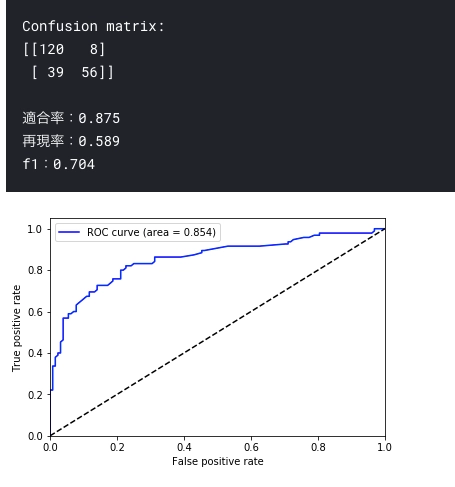

おっ。ランダムフォレストが負けてる？

再現率がさらに低いな。。

AUC でもわずかに劣ってる。 ただ、ROC の形状的にはランダムフォレストのほうがよさそう？？

なんだか予想がきかないデータが一定数ある気がする。外れ値的なやつかな。

いや、ランダムフォレストの結果をみると、ラベルに偏りがありそう。 サンプリングのランダム性を収束させるために回数まわして平均とったほうがいいかも。

Kaggle でテスト結果を提出してみた

やり残しというか、まだまだ考慮すべきことはあるが、ここまできたらテストデータに対するスコアをみてみたい。 ということで、Kaggle で初提出してみた。

コード中のtest_dataはtrain_dataと同様の処理をして作った。 （テストにしかない欠損があったのでそこは別途埋める必要あり）

result = lgr.predict(test_data)
#result = rf.predict(test_data)
submission = pd.DataFrame({
        "PassengerId": test_data_copy["PassengerId"],
        "Survived": result
    })
submission.to_csv("submission.csv", index=False)

これで Commit して終了。

結果はこんな感じでした。

title: 【機械学習】初心者がKaggleのtitanicで勉強してみた(モデル評価編) createdAt: '2019-03-10' updatedAt: '2019-03-10' tags: '機械学習' draft: false description: '' thumbnail: '/img/twitter-card.png'

【機械学習】初心者がKaggleのtitanicで勉強してみた(モデル評価編)

結局、ランダムフォレストの方がよかった。

実は、前節でのスコアはたまたまで、数回試したらほとんどの場合ランダムフォレストのほうが性能がよかった。

反省点

これまでの反省点まとめます。

まず前処理編で作ったパイプラインは作らなくてよかった。

それぞれクラスにする必要性は感じなかったし、クラスももっと柔軟に変更できるようにすべきだった。 あのようなパイプラインを作った理由の一つに、データが DataFrame のままだとモデルに投入できないと思っていたことがある。 しかし、DataFrame で普通にできることに途中で気づいた。

前処理と特徴量エンジニアリングで想像以上にデータ変更の機会が多く、ここは最初にそんなに作り込むべきではないと思った。 少なくとも、素人が最初にやらないほうがいいと思う。

とりあえず、モデルの検証までやって、特徴量をいじりながら効率的な方法を模索しながらやったほうが時間がかからなかったように思える。 慣れてくれば、汎用的な関数なりクラスを作ってのぞむ感じがよさそう。

まとめ

ようやく Titanic 卒業しました。

機械学習の入門編ということでやってましたが、ひじょーーーーーーーに勉強になった。 Titanic ちゃんとやるとほんとに難しいし、学びも多い。 というかわからないことが多すぎた。

とくに特徴量エンジニアリングはかなり悩んだ。他の人の解説等をみてもどういう根拠に基づく処理なのかわからず、理解するのに時間がかかった。 記事内には書いてないが、かなりいろいろ試してます笑

web 上のコードを調べると Name から Mr とかを抽出して特徴量にするアプローチがあったんですが、今回はやらないことにしました。 理由は、自分でまったく思いつかなかったことで悔しかったからです笑

最終的なスコアが低いのかと思っていたが、これって問題の難しさに依存するのでそこまで気にしなくていいのではと思い始めた（あきらめ）。 Kaggle 内の順位とは関係なしに考えると、生存者予測で 8 割近い精度ならまあまあ予測できていると思う。

次は Deep なほうを勉強していきます！

参考書籍

• scikit-learn と TensorFlow による実践機械学習
• Python ではじめる機械学習 ―scikit-learn で学ぶ特徴量エンジニアリングと機械学習の基礎